A. Teitelman of Israel, John Snyder of Oconomowoc WI, Philippe Fondanaiche of Paris (France), Dan Dima of Constanta (Romania), and Bojan Basic of Novi Sad (Serbia) provided solutions. Most noted that this was a well-studied problem with a seminal paper by R. H. Buchholz (see reference [2]). Using the labeling scheme shown below (figure due to John Snyder), here is a table of some heronian tetrahedra, the areas of their faces, and their volumes. Note that the first entry has the smallest possible maximal side length, the second has the smallest possible surface area and volume, the next two have congruent faces, and the remainder have faces that are right triangles.
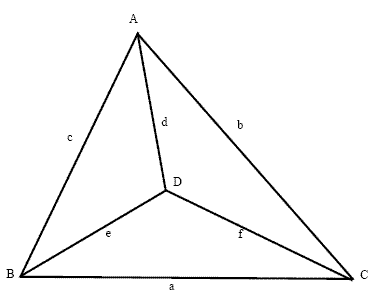
| a | b | c | d | e | f | abc | aef | bdf | cde | V |
| 51 | 52 | 53 | 80 | 117 | 84 | 1170 | 1890 | 2016 | 1800 | 18144 |
| 25 | 39 | 56 | 120 | 160 | 153 | 420 | 1872 | 1404 | 2688 | 8064 |
| 148 | 195 | 203 | 148 | 195 | 203 | 13650 | 13650 | 13650 | 13650 | 611520 |
| 533 | 875 | 888 | 533 | 875 | 888 | 223860 | 223860 | 223860 | 223860 | 37608480 |
| 104 | 153 | 185 | 697 | 672 | 680 | 7956 | 34944 | 52020 | 62160 | 1782144 |
| 264 | 448 | 520 | 975 | 1105 | 1073 | 59136 | 141636 | 218400 | 253500 | 19219200 |
Philippe Fondanaiche's exposition is here (in PDF format).
References