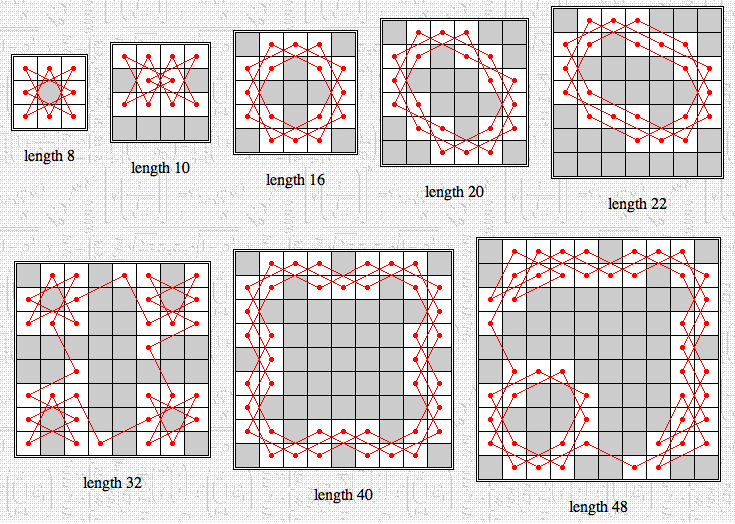
Erich Friedman points out that if one asks in addition that the "knight's graph" be connected, then Jonathan Welton has solved the problem for n = 3, 4, ..., 10 (see below).
For other related questions and results, see Erich Friedman's Math Magic page here.

Jonathan Welton notes that if we consider rectangular boards, then there are disconnected graphs that have more vertices than connected ones in the 4×12 and 4×16 cases (see below).
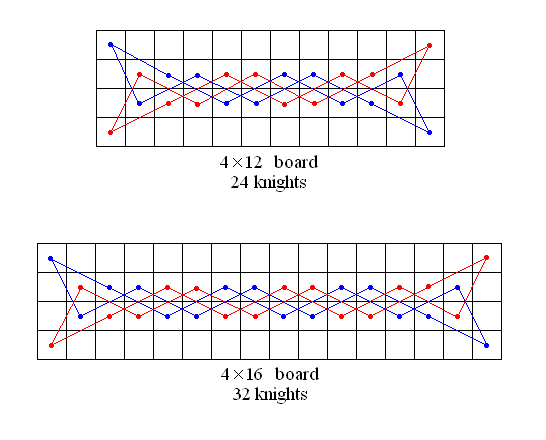
Kirk Bresniker produced the following example of a disconnected graph with 24 vertices, which has more vertices than the maximal connected graph (which has 22 vertices)
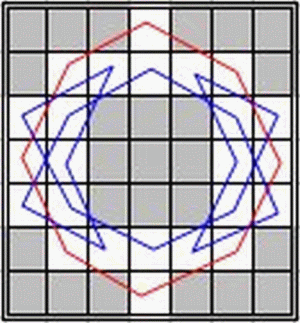
Further results are solicited.