Bojan Basic of Novi Sad (Serbia), Philippe Fondanaiche of Paris (France), and Christian Bau made contributions to this problem. Here is Christian Bau's approach followed by Bojan Basic's remarks.
Solution: n = 3 is trivial (equilateral triangle); assume n >= 4. For d = 1, 2, 3 etc.
we try to find n points at integer distances with no distance greater than d. Assume
that point 1 is at (0, 0) and point 2 is at (0, d). All the other points must be at an
integer distance from these two points. So for all integers a, b such that a + b > d
and a <= d, b <= d, find the two points that are at a distance a from (0, 0) and at
a distance b from (0, d). These points meet the two equations:
x^2 + y^2 = a^2
x^2 + (d - y)^2 = b^2
We find easily that y = (d^2 + a^2 - b^2) / 2d and x = +/- sqrt (a^2 - y^2). For
fixed d, there are roughly (d^2 / 2) combinations of distances a and b to consider
and roughly d^2 points at integer distances <= d away from the first two points.
For n <= 10, we can easily do an exhaustive search to find all pairs of these points
that are at an integer distance from each other, then all triples, sets of four
points and so on. This search finds:
d (4) = 4; p3 = (1.45237, 1.375), p4 = (-1.93649, 3.5)
d (5) = d (6) = 8; p3, p4 = (2.59808, 4 +/- 2.5), p5, p6 = (-4.33013, 4 +/- 1.5)
d (7) = 33, p3, p4 = (9.68246, 16.5 +/- 14), p5, p6 = (-13.5554, 16.5 +/- 8),
p7 = (17.4284, 16.5)
d (8) = d (9) = 56, p3, p4 = (-18.1865, 28 +/- 17.5), p5, p6 = (30.3109, 28 +/- 10.5),
p7 = (15.8359, 2.28571), p8 = (-24.125, 30.6429), p9 = (20.4135, 51.0714)
d (10) = 105, p3, p4 = (42.4352, 52.5 +/- 28), p5, p6 = (-48.4974, 52.5 +/- 24.5),
p7 = (10.8872, 1.57143), p8 = (-36.7442, 13.0714), p9 = (49.4872, 42.1429),
p10 = (-52.5801, 66.7857).
For larger n, the exhaustive search compares any of about d^2 points with any other of
those points and checks whether the distance is an integer; this takes about d^4 operations,
which is fine for n = 10, d(n) = 105, but doesn't work well for much larger values. The
search can be made significantly faster: Instead of checking whether the distance of two
points is an integer, we check for the necessary condition that the distance it is the
square root of a rational number: For any (a, b), the point at distance a from (0, 0)
and distance b from (0, d) is at (x, y), where y is a rational number and x is the square
root of a rational number. If we take two points (x1 = sqrt (s1), y1) and (x2 = sqrt (s2), y2),
then we need (x1 - x2)^2 to be rational, which is the case if 2 (x1 * x2) is rational or
s1 * s2 is the square of a rational number.
Given a, b, we find x = +/- sqrt (4a^2 d^2 - (d^2 + a^2 - b^2)^2) / 2d. The quotient 2d
is independent of a and b. Define f (a, b) = d^2 + a^2 - b^2, g (a, b) =
(2ad)^2 - f (a, b)^2. The distance between the points for two different distances (a, b)
is the square root of a rational number if and only if the product of the two values
g (a, b) is a square. Define h (a, b) = g (a, b) divided by its largest square factor.
Then the distance between two points is the square root of a rational number only if the
two values h (a, b) are the same.
So here is a faster algorithm to find d (n):
Assume n >= 4. Iterate for d = 1, 2, 3 and so on until a solution is found. For each
d: For a = 1 to d and for b = d - a + 1 to d calculate f (a, b) = d^2 + a^2 - b^2,
g (a, b) = (2ad)^2 - f (a, b)^2, then h (a, b) = g (a, b) divided by its largest square
factor. Sort by the value of h (a, b) and find all sets of pairs (a, b) where the value
of h (a, b) is the same. For each of those sets perform an exhaustive search for sets
of n-2 points at integer distances <= d. For each set found add the points (0, 0) and
(0, d) and check that no three points in a set are on the same line. In that case a
solution has been found.
Bojan Basic points out that the is a research problem that is still open. So far it is known that there exist constants c1 and c2 such that
by [1] and [2], respectively. Exact values of d(n) are known only for 1 ≤ n ≤ 9:
In an unpublished note [4] S. Kurz and A. Wassermann claim to have the exact values of d(n) determined up to n = 36:
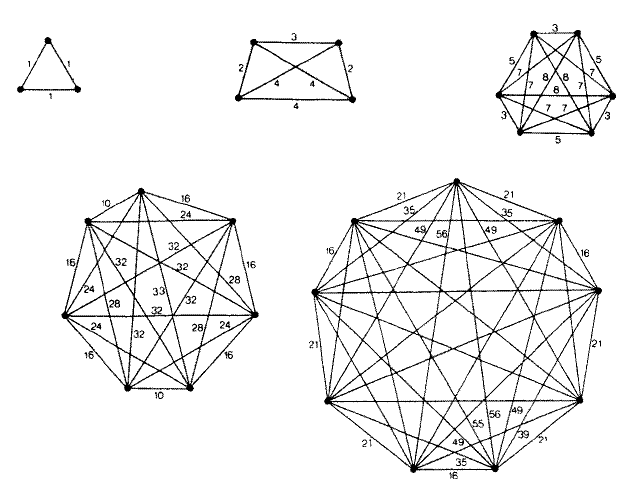
The picture below (reproduced from [2]) shows configurations for n = 3, 4, 6, 7, and 9

References