Solution to Problem #2



Ignacio Larrosa Caņestro of Coruņa (Spain), Vince Lynch of Doncaster (UK), L.T. Pebody of NYC/Cambridge/Princeton, Ross Millikan of San Mateo CA, Al Zimmermann of Lausanne (Switzerland), Matt Hudelson of Washington State University, David Blackston of Berkeley CA, Nancy Schwarzkopf of New York NY, Ajit Thyagarajin of Silver Spring MD, Philippe Fondanaiche of Paris (France), Darryl Nester of Bluffton College, Alexey Vorobyov of Irvine CA, Vivek Kumar Mehra of Mumbai (India), Bobby Varghese of IIT Bombay (India), Susan Hoover of Houston TX, and Lou Poulo of Andover MA solved the problem.

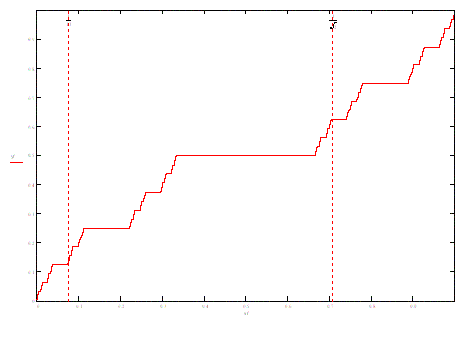
Many solvers pointed out that F(x) is the Cantor ternary function whose graph is sometimes referred to as the "Devil's Staircase". Lou Poulo provided the image below.

Here is L.T. Pebody's solution: 

a) F(1/13)=1/7

 Proof: Let a=f(1/13), b=f(3/13), c=f(4/13)

Then 2a=f(3/13)=b, 2b=f(9/13)=1-c and 2c=f(12/13)=1-a.

Therefore : 8a=4b=2-2c=1+a. That is to say that a=1/7.

b) F(Sqrt[1/2])=5/8

Note that 19^2=361, 20^2=400 and 27^2=729. Note further that
361<(729/2)<400.

Therefore 19/27<Sqrt[1/2]<20/27.

Now F(0/3)=F(0)/2, so F(0)=0.
F(0)+F(1)=1, so F(1)=1.

F(1/3)=F(1)/2, so F(1/3)=1/2.
F(1/3)+F(2/3)=1, so F(2/3)=1/2.

F(1/9)=F(1/3)/2, so F(1/9)=1/4.
F(2/9)=F(2/3)/2, so F(2/9)=1/4.

F(1/9)+F(8/9)=1, so F(8/9)=3/4.
F(2/9)+F(7/9)=1, so F(7/9)=3/4.

F(8/27)=F(8/9)/2, so F(8/27)=3/8.
F(7/27)=F(7/9)/2, so F(7/27)=3/8.

F(8/27)+F(19/27)=1, so F(19/27)=5/8.
F(7/27)+F(20/27)=1, so F(20/27)=5/8.

Therefore 5/8=F(19/27)≤F(Sqrt[1/2])≤F(20/27)=5/8.


Back to the Archives
Back to the Math Department Homepage.