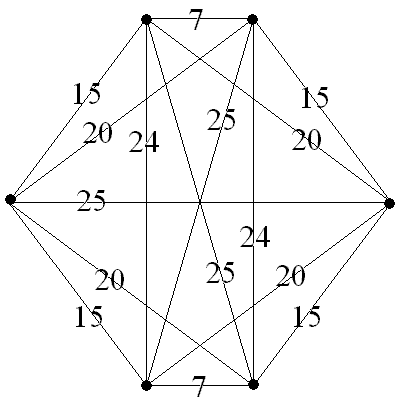

This month's problem involves placing n distinct points in the plane so that no three of them lie on a line and all of the distances between them are integers. Such a configuration is shown for n = 6 in the diagram below. Let d(n) denote the minimum possible value of the largest distance for such a configuration of n points. Clearly d(3) = 1 (equilateral triangle) and the figure below shows that d(6) ≤ 25. Find d(4), d(5), d(6), d(7), and d(8) (or provide your best estimates). What can you say about the asymptotic behavior of d(n) (if anything)?
