Problem #9

You are given four transformations of a 3×3 grid:
- A takes the 2×2 square in the upper left-hand corner and
rotates it 90 degrees clockwise.
- B takes the 2×2 square in the upper right-hand corner and
rotates it 90 degrees clockwise.
- C takes the 2×2 square in the lower left-hand corner and
rotates it 90 degrees clockwise.
- D takes the 2×2 square in the lower right-hand corner and
rotates it 90 degrees clockwise.
For example the result of performing transformation A followed by
transformation D is shown below.
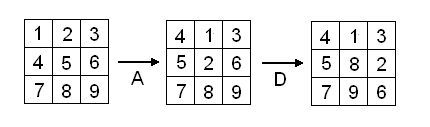
-
Show that begining with the grid numbered as above, any permutation of the
numbers can be realized by a finite sequence of A's, B's,
C's and D's.
-
Find the shortest possible sequence of such transformations
that will switch the positions of "1" and "9" while leaving the remaining
numbers fixed.
-
What is the least number n such that any permutation can be
realized by a sequence of n or fewer transformations?


