Problem #6

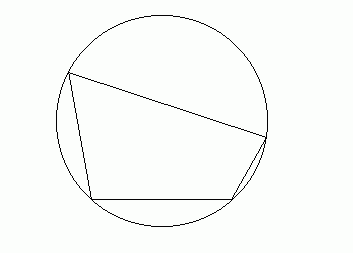
A cyclic quadrilateral is a quadrilateral which can be inscribed in
a circle (see figure below). Rectangles and isosceles trapezoids are
examples of cyclic quadrilaterals. This month's problem is to find all
cyclic quadrilaterals having sides of integer length such that the area of
the quadrilateral is numerically equal to the perimeter.