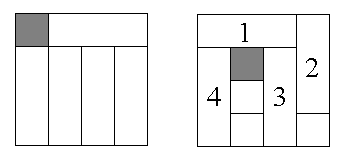

Let n be a positive integer that is not a multiple of 3. Which single squares can be removed from an n×n checkerboard so that the remaining squares can be covered by straight trominoes (1×3 rectangles) without overlap? For example, in a 4×4 board, one can cover the region obtained by removing a corner square, but one cannot cover the region obtained by removing a square on the diagonal next to a corner square. A successful tiling is shown on the left and a forced non-tiling is shown on the right (the number in a tromino indicates the order in which it is laid down).
