Solution to Problem #88

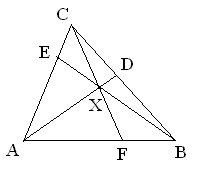Since triangle AXE and triangle CXE have the same altitude, the ratio of their areas equal to the ratio of their bases (i.e. 45:35 = 9:7). But the same argument applies to triangle ABE and triangle BCE, so the ratio of their areas is the ratio of their bases, which we've seen is 9:7. Denoting the area of triangle BXF by S, the area of triangle BXD by t, and the area of triangle CXD by u, we have

(s + 60 + 45)/(t + u + 35) = 9/7.

Similarly, by examining the triangles whose bases lie on side BC, we have

(60 + s + t)/(45 + 35 + u) = t/u,

and the triangles whose bases lie on side AB yield

(s + t + u)/(60 + 45 + 35) = s/60.

After simplification these three equations become

−7 s + 9 t + 9 u = 560
80 t − 60 u = su
4 s − 3 t − 3 u = 0

Adding three times the first equation to the third eliminates t and u and we obtain s = 84. Making this substitution into the second and third equations and simplifying yields

9 u = 5 u
t + u = 112

and hence t = 72 and u = 40.