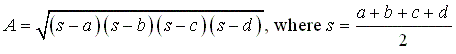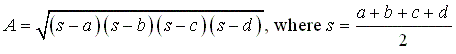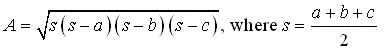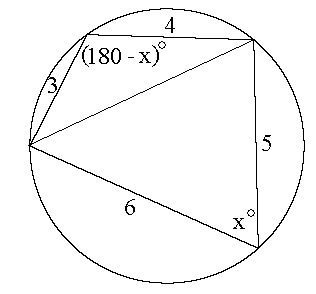Solution to Problem #60
There is a very beautiful formula that states that the area of a
quadrilateral with sides a, b, c, and d that
is inscribed in a circle is
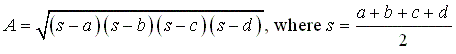 Note the similarity to Heron's formula for the area of a triangle with
sides a, b, and c:
Note the similarity to Heron's formula for the area of a triangle with
sides a, b, and c:
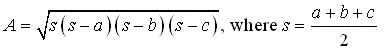 However, since the formula above is not well-known, we'll find the answer
by other methods. Since the quadrilateral is inscribed in a circle,
opposite angles are complementary. Applying the Law of Cosines to the
angles with measures x degrees and 180 - x degrees in the
figure below, we have 3^2 + 4^2 -2*3*4*Cos[180-x] = 5^2 + 6^2
-2*5*6*Cos[x] and Cos[180-x] = -Cos[x], so
Cos[x] = 3/7. Therefore
Sin[x]
= Sqrt[1 - Cos[x]^2] = Sqrt[1-(3/7)^2] = Sqrt[40/49] =
2*Sqrt[10]/7.
However, since the formula above is not well-known, we'll find the answer
by other methods. Since the quadrilateral is inscribed in a circle,
opposite angles are complementary. Applying the Law of Cosines to the
angles with measures x degrees and 180 - x degrees in the
figure below, we have 3^2 + 4^2 -2*3*4*Cos[180-x] = 5^2 + 6^2
-2*5*6*Cos[x] and Cos[180-x] = -Cos[x], so
Cos[x] = 3/7. Therefore
Sin[x]
= Sqrt[1 - Cos[x]^2] = Sqrt[1-(3/7)^2] = Sqrt[40/49] =
2*Sqrt[10]/7.
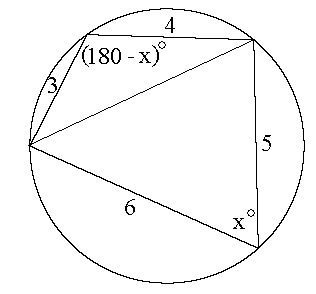 Now
the area of the triangle containing the angle with measure x is
(1/2)*5*6*Sin[x] = 30*Sqrt[10]/7 and the other triangle has area
(1/2)*3*4*Sin[180-x] = 12*Sqrt[10]/7. Therefore the area of the
quadrilateral is (30+12)*Sqrt[10]/7 = 6*Sqrt[10] square units.
Now
the area of the triangle containing the angle with measure x is
(1/2)*5*6*Sin[x] = 30*Sqrt[10]/7 and the other triangle has area
(1/2)*3*4*Sin[180-x] = 12*Sqrt[10]/7. Therefore the area of the
quadrilateral is (30+12)*Sqrt[10]/7 = 6*Sqrt[10] square units.