

Define regions 1 and 2 above and below the x-axis respectively, as shown in the diagrams. The area components A1 and A2 and volume components V1 and V2 can be found as follows:
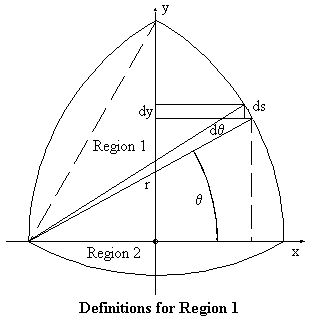
Region 1, with theta from 0 - pi/3:
x = r cos(theta) - r/2 = r(cos(theta) - 1/2), ds = r d(theta), dy = cos(theta) ds = r cos(theta) d(theta).
dA1 = 2 pi x ds = pi r2 ( 2 cos(theta) - 1) d(theta)
dV1 = pi x2 dy = pi r3 ( cos(theta) - 1/2)2 cos(theta) d(theta).
Integrating over 0 - pi/3 gives:
A1 = pi r2 (sqrt(3) - pi/3)
V1 = pi r3 (3 sqrt(3)/8 - pi/6)
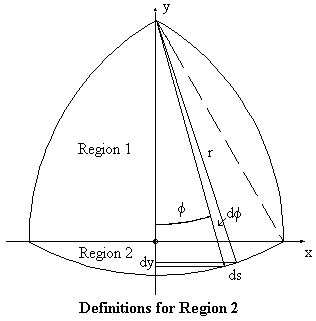
Region 2, with phi from 0 - pi/6:
x = r sin(phi), ds = r d(phi), dy = sin(phi) ds = r sin(phi) d(phi).
dA2 = 2 pi x ds = 2 pi (r sin(phi)) r d(phi) = 2 pi r2 sin(phi) d(phi),
dV2 = pi x2 dy = pi (r sin(phi))2 r sin(phi) d(phi) = pi r3 sin3(phi) d(phi).
Integrating over 0 - pi/6 gives:
A2 = pi r2 (2 - sqrt(3))
V2 = pi r3(2/3 - 3 sqrt(3)/8)
Combining for the totals,
Area = pi r2 (2 - pi/3),
Volume = pi r3 (2/3 - pi/6).