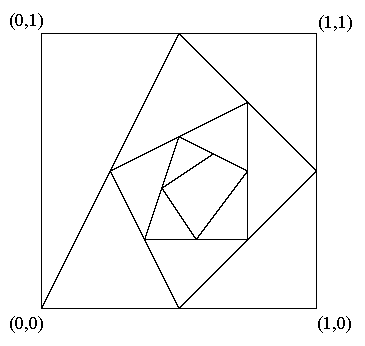
Problem #49

A spiral path is constructed in the unit square whose vertices have
coordinates (0,0), (1,0), (1,1), and (0,1) as follows. Let A1
= (0,1), A2 = (1,1), A3 = (1,0), and A4 =
(0,0). Let A5 be the midpoint of A1A2,
A6 be the midpoint of A2A3, A7
be the midpoint of A3A4, etc. This forms a spiral
polygonal path A1A2A3A4...
converging to a unique point in the plane. Find the coordinates of this
point.
Source: Len Bos and Bill Sands


